Лекция 5 - Корелация ≠ каузалност

Абсурдът на данните

Ако ви кажа, че има връзка между Тейлър Суифт и употребата на изкопаеми горива в Британските Вирджински острови, вероятно не бихте ми повярвали. Нека обаче да погледнем тази графика:

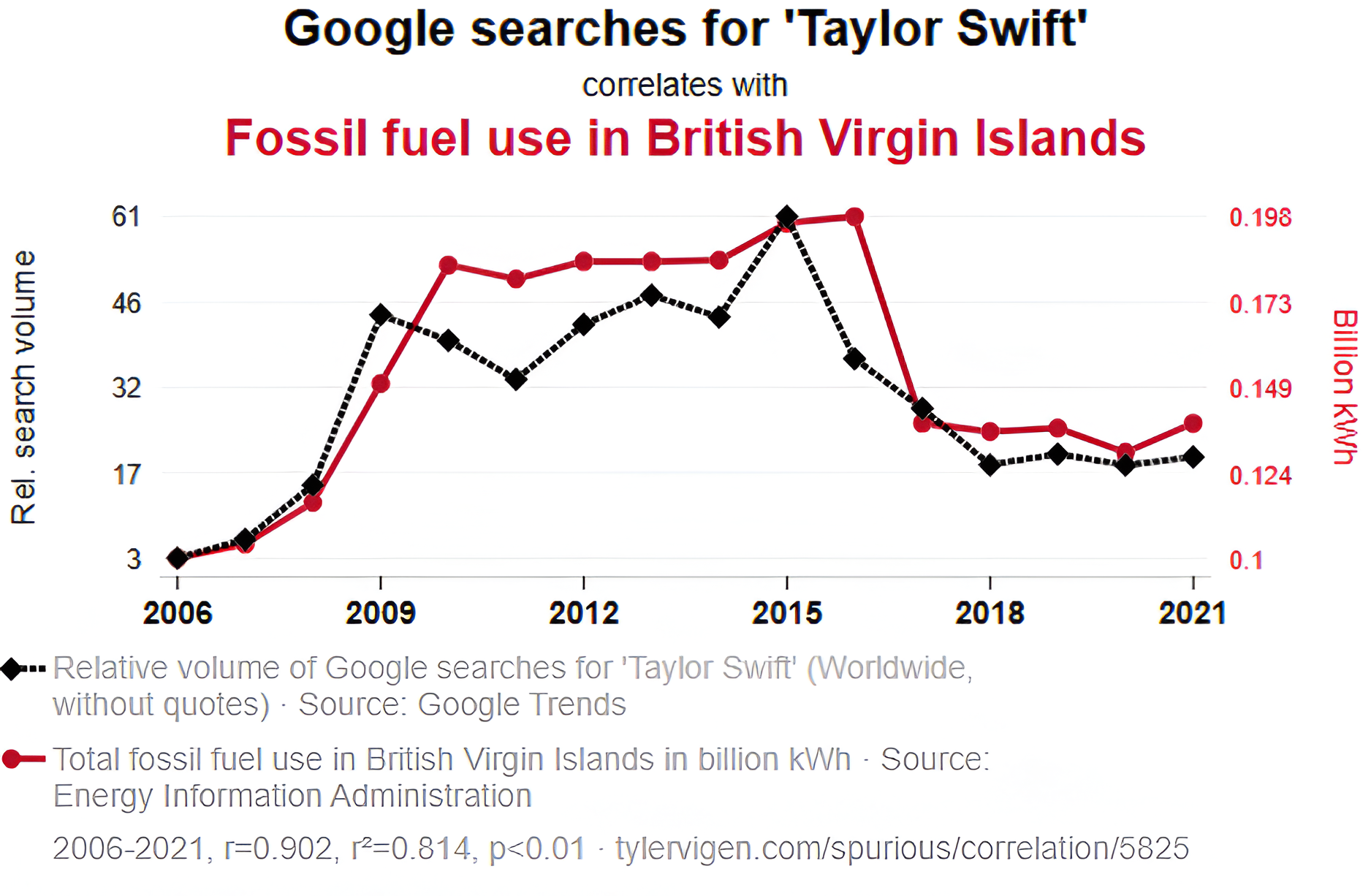
Еха, тя е успяла собственоръчно да понижи употребата на горива с 25% между 2015 и 2018 г. Наистина впечатляващо!
Ако обаче спрем да се шегуваме и бъдем четсни за момент, трябва да признаем, че това е просто съпоставка между два различни вида данни, чиито шанс да имат нещо общо помежду си е нула.
Корелацията (връзката) между две променливи невинаги е знак, че те са взаимносвързани, и че промяната в едната променлина причинява промяна у другата. Това е доста груба (но не толкова рядко срещана) грешка, която може да накара и най-нелепите връзки да изглеждат валидни.
Въпреки потенциалните си неточности, корелацията между две несвързани променливи не е напълно безполезна. Чрез нея могат да се правят прогнози или пък да се подскаже за трета променлива, която е повлияла върху резултатите, но не е била измерена. Чисто хипотетично е възможно концертът на Тейлър Суифт на Британските острови през 2015 да е бил причината да се повиши драстично редовната употреба на охладителни тела, за да освежат страстите. Поради тази причина може да се е вдигнала и консумацията на изкопаеми горива. Така по един индиректен начин може да бъде доказана нашата корелация. Но, но, корелации, чиито променливи не притежават причинно-следствена връзка, а са свързани с трета, се наричат фалшиви корелации.

Посоката има значение

Освен да обръщаме внимание само на каузалността при променливите обаче, е важно да наблегнем и върху техните отношения. Ако две променливи са директно свързани, те имат правопропорционална корелация, тоест с повишаването на едното се повишава и другото. Могат да имат и директна обратнопропорционална корелация, тоест с повишаването на едното да се понижава другото. Освен това има и още един поддетайл, който е от съществено значевие за една валидна корелация, и това е именно посоката на отношенията (между променливите).
Макар и абсурден, ето ви и още един пример:
Ако след консумацията на алкохол, се увеличават шансовете за пътни произшествия, то ние може да заключим, че алкохолът вреди на ситуацията. Грешно-разчетената интерпретация пък би била, че след катастрофа, шофьорите са склонни по-често да си сипват по една или две чашки, за да им мине болката.
В конкретния пример е лесно да се определи посоката на корелацията, но е важно и при по-особените случаи да внимаваме с преценката си. Всяка грешка би била еквивалента на това да смятаме пътната катастрофа като причина за алкохола.

Уклон на селекцията

Този уклон се проявява при взаимодействието между изследваното лице и средата. Възниква, когато хора с различни личностни, биологически и поведенчески характеристики избират различни типове среда. Доста завоелирано определение, което може да бъде доста просто демонстрирано:
Ако хипотетично град Добрич има процент над средния за смъртни случаи поради респираторни заболявания, ние бихме си помислили, че има нещо нередно във въздуха, който е из града и около него. Но това не е единственото валидно обяснение. В случая град Добрич може да е доста чист и алтернатива за обяснението на смъртността да бъде, че гражданите на София, болни от респираторни заболявания, са решили да се прибират в Добрич и да умрат там.
Отново, трябва да се внимава, тъй като има случаи, в които факторите на селекцията не са толкова лесно уловими и е възможно да се направят фатални заключения. Ако има едно нещо, което трябва да запомним, то е, че уклонът на селекцията създава фалшива корелация между средата и поведенческо-биологичните характеристики на дадения човек. За да се елиминира това е необходимо да се проведе легитимен експеримент, в който променливите могат да бъдат манипулирани от експериментатора.