Лекция 2 - Логика, продължение

Категорични Твърдения

След като разбрахме основите на логиката, е време да продължим със същинската част. А 90% от същинската част се състои в категорични твърдения. Какво представляват те?

Най-просто казано категоричните твърдения са твърдения, които или са истина, или не са. Логиката работи с термини и ролята на категоричните твърдения е да покажат дали има връзка между два или повече термина. Преди обаче да ви обясня как се случва това, искам да въведа 2 нови понятия в нашия речник - субект и предикат (S и P). Мислете за тях като за подкатегория и надкатегория. Например: куче → субект; животно → предикат.

Субектът е част от предиката. Но в зависимост от това точно каква част от предиката заема, категоричните твърдения го разделят на 4 вида:

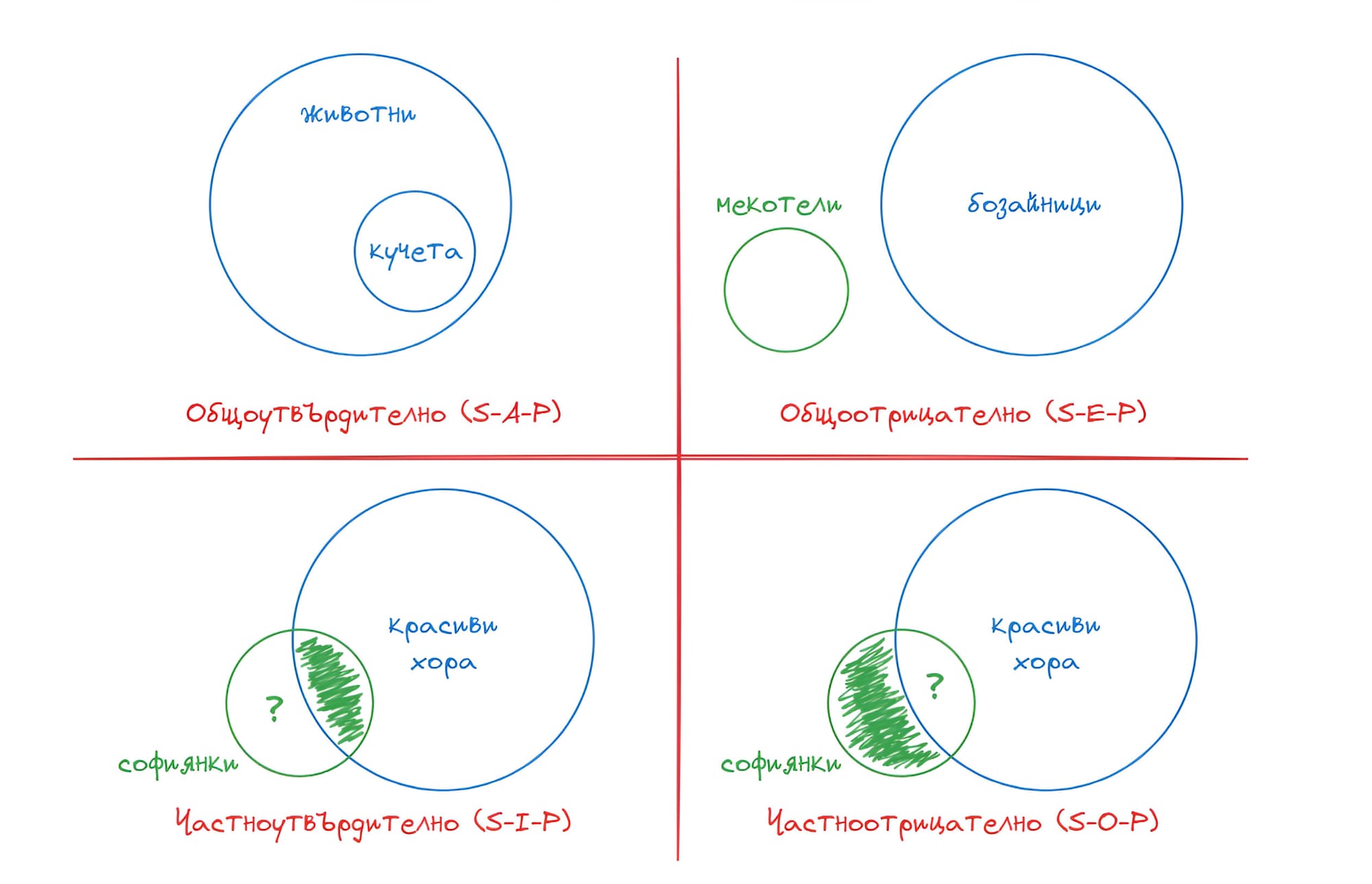
Общоутвърдително съждение - всеки един субект е част от предиката - например всяко “куче” е част от категорията “животни” (S-A-P)
Общоотрицателно съждение - нито един субект не е част от предиката - например нито едно “мекотело” не е част от категорията “бозайници” (S-E-P)
Частноутвърдително съждение - някои субекти са част от предиката - например някои “софиянки” със сигурност попадат в категорията “красиви хора” (S-I-P)
Частноотрицателно съждение - някои субекти не са част от предиката - някои “софиянки” със сигурност не попадат в категорията “красиви хора” (S-O-P)

Логически квадрат

4-те категорични твърдения, за които говорихме досега, са в постоянно връзка помежду си (като мускетарите). По този начин, заедно те образуват така наречения “логически квадрат”.

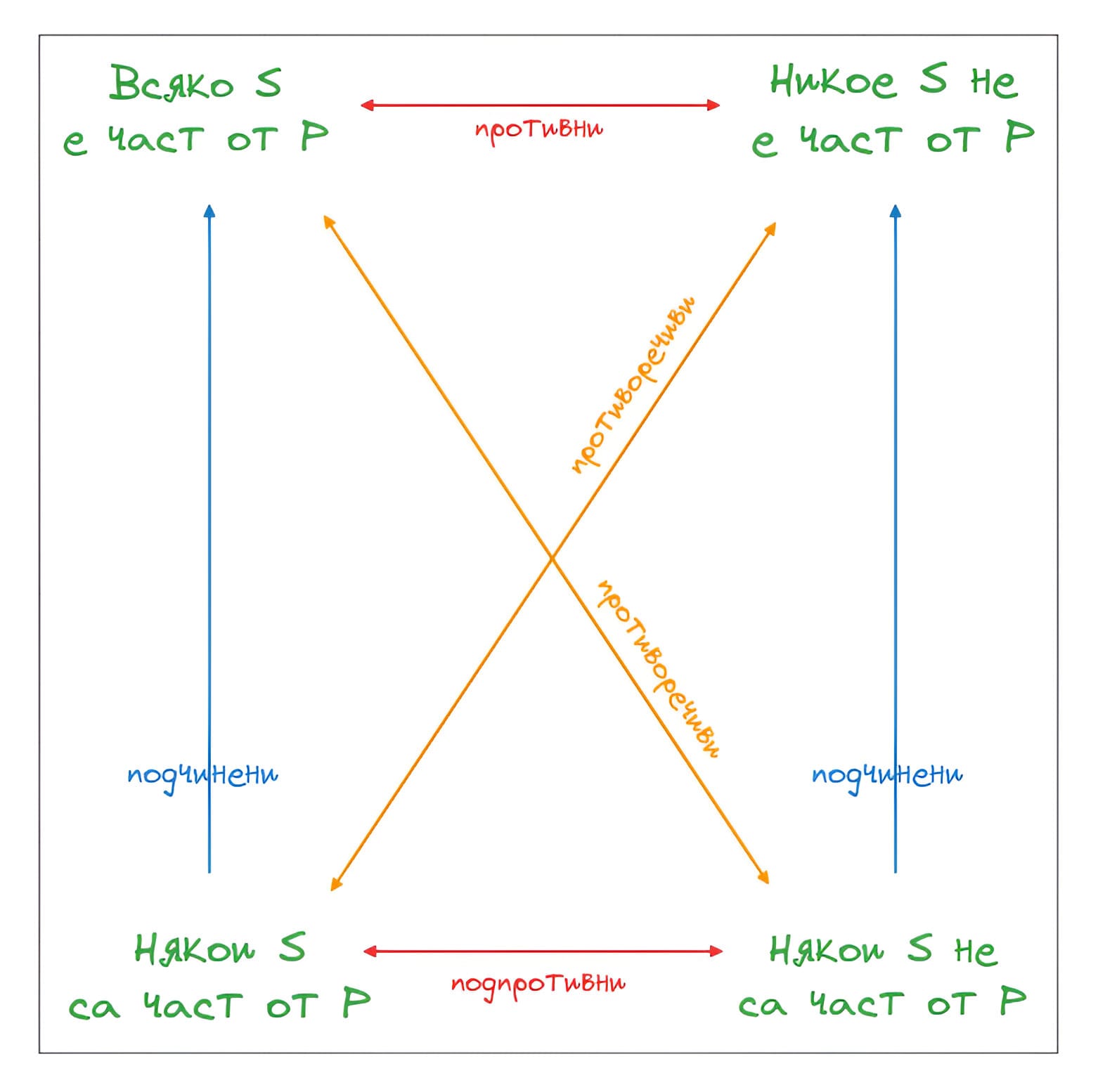
Такаа, може би този квадрат изглежда леко хаотично и разбъркано, но нека ви обясня с прости думи как работи той.

Първо, най-отгоре на квадрата, в двата ъгъла имаме твърденията SAP и SEP (всяко S е Р и нито едно S не е Р). Между тях има стрелкичка, на която пише “противни”, защото те са именно такива. Едното е обратното на другото.

Под тях двете, в долните два ъгъла, имаме SIP и SOP (някои S са Р и някои S не са Р). Те отново са противни едно на друго, но също така са и подчинени на горните две твърдения. Ако SAP е вярно, то тогава и SIP е вярно. Ако SEP е вярно, то тогава и SOP е вярно.

Накрая, виждаме как по диагоналите на квадрата пише “противоречиви”. Това означава, че ако едното от двете твърдения е правилно, то няма как и другото да е правилно. Или това в горния ляв ъгъл ще е истина, или това в долния десен ъгъл ще е истина. Или това в горния десен ъгъл ще е истина, или това в долния ляв ще е истина.

Искам още веднъж да обърна внимание - противни и противоречиви са две различни неща. “Противни” означава, че едното е обратното на другото. “Противоречиви” означава, че няма как и двете да са истина.

Ако 2 твърдения са противни, те могат да бъдат неистинни едновременно, но не могат да бъдат истинни едновременно.

Ако 2 твърдения са противоречиви, те не могат да бъдат нито истинни, нито неистинни едновременно. Само едното от тях може да бъде.

Давам ви и бонус конкретен пример за яснота:

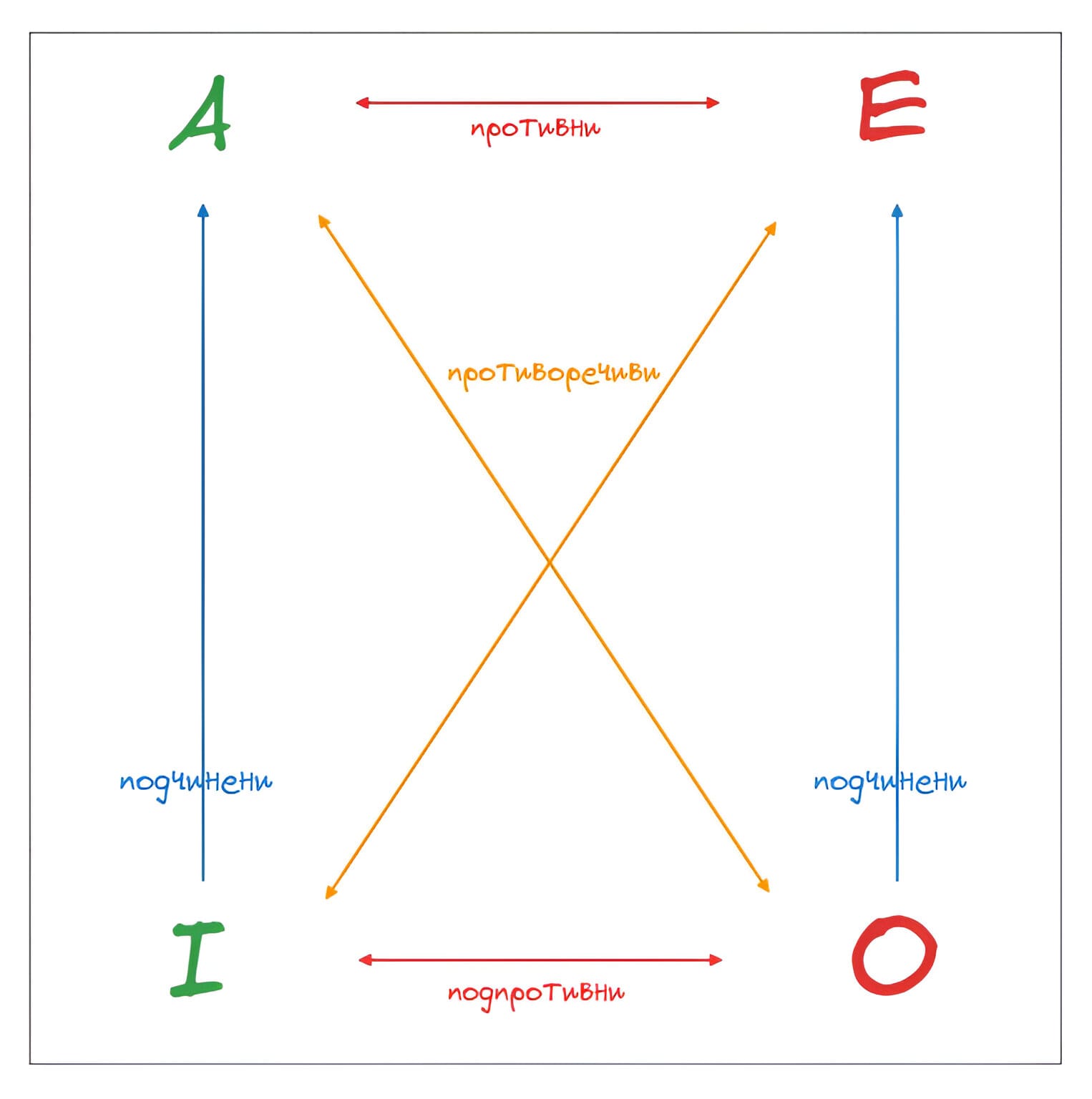
Да приемем, че в следния пример А е истина. То тогава I също е истина, а Е и О са лъжа.

Категоричен силогизъм

Категоричен силогизъм означава, че имаме 3 твърдения, като първите 2 са предпоставка и третото следва от тях със сигурност. Затова се и нарича “категоричен” силогизъм.

Та такаа, нека първо вземем следния пример:

Всички блондинки са глупави.
Всички красавици са блондинки.
Следователно, всички красавици са глупави.

*Преди да продължа, искам да споделя, че познавам множество интелигентни блондинки, и въпреки примера, аз нямам предразсъдъци.

Нека сега раздробим горния израз на съставните му части.

Всички блондинки са глупави.
Всички красавици са блондинки.
Следователно, всички красавици са глупави.

В горния израз имаме точно 3 термина - това са красивици, блондинки, и глупави.

Красавица е най-малкият термин. (S - субект)
Блондинка е средният термин. (М - междинен)
Глупава е най-големият термин. (Р - предикат)

Ако се чудите по какво точно се определя размерът на един термин, то това е просто следствие от начина, по който са подредени термините в изречението. В случая думата красавици е подкатегория на групата блондинки, а блондинки е подкатегория на думата глупави. Това е.

Така, продължавайки по-нататък, нека отбележим, че категоричният силогизъм може да бъде точно 4 вида, или както се наричат в логиката - 4 фигури.

В първата фигура междинният термин е на първа позиция (в първо изречение) и на втора позиция (във второ изречение).

Всички блондинки са глупави.
Всички красавици са блондинки.
Следователно, всички красавици са глупави.

Във втората фигура междинният термин е на втора позиция (в първо изречение) и на втора позиция (във второ изречение).

Всяка жена е умна.
Нито една маймуна не е умна.
Нито една жена не е маймуна.

В третата фигура междинният термин е на първа позиция (в първо изречение) и на първа позиция (във второ изречение).

Всички мъже са силни.
Всички мъже са бързи.
Някои силни хора са и бързи хора.

В четвъртата фигура междинният термин е на втора позиция (в първо изречение) и на първа позиция (във второ изречение).

Всички жени са хитри.
Всички хитреци са добри готвачи.
Някои жени са добри готвачи.

В допълнение към казаното, искам да добавя и още една нова дума. Тя се казва модус. Може би сте забелязали как постоянно пиша “всички, никои, някои”. Е, модусът служи за съкращение на тези думи.

Например модус AAA означава “Всички … → Всички … → Следователно всички …”.

Модус EIO означава “Нито един … → Някои … → Следователно някои … не са … ”.

А - Всички … са …
Е - Нито един … не е …
I - Някои … са …
O - Някои … не са …

И като за финал към категоричните силогизми, ето ви всички възможни комбинации от модуси и фигури (не се опитвайте да ги помните, безсмислено е, дори аз не ги знам):

1-ва фигура - AAA, AAI, EAE, AII, EIO

2-ра фигура - EAE, AEE, EIO, AOO

3-та фигура - AAI, IAI, AII, EAO, OAO, EIO

4-та фигура - AAA, AAI, AEE, IAI, EAO, EIO

Това е средносложната част от логиката. Мисля, че ще се справите :)