Лекция 2 - Кривата на Гаус

*За улеснение ще използвам съкращението ЕП (експериментална психология) на някои места

Кои данни са най-ценни в експерименталната психология?

Всеки от нас има различен опит. Това го оформя като отделна личност с уникални преживявания. Не е толкова трудно да открием двама души с различни мнения по един и същи въпрос (много често 2 противоречащи си мнения дори могат да идват от един и същи човек :д).
Точно поради тази причина ние буквално сме заляти от информация. Един казва едно, друг казва друго, а в интернет пише трето. Трудно можем да боравим с цялата тази информация и да си правим адекватни изводи за света около нас без инструментите на ЕП. Какви са тези инструменти, сигурно ще попитате? Това ще ви го кажа малко по-нататък. Първо нека обърнем внимание на въпроса каква информация успяват да докопат тези инструменти.
В ЕП най-често (но не винаги) от първостепенно значение е информацията за типичното изпълнение на дадена задача. Казано с прости думи, ЕП се интересува от това какво ще се случи в най-общия случай. Винаги ще има изключения от правилото, но за да можем да правим точни предположения, и да сме прави възможно най-често, ние имаме нужда точно от информацията за типичното изпълнение. Типичното изпълнение е най-качествената мярка за доказване на дадена хипотеза.
Преди да преминем към научната част, първо ще ви дам пример как тази информация може да се използва във вашия личен живот. Всеки от нас например има по един приятел, който винаги изкарва отлична оценка на тестовете си в университета, макар и да твърди, че според него се е справил ужасно. Да, понякога изкарва 5, или 4, но в края на семестъра успехът му отново е 6.00. Малко дразнещо, а? Както и да е. Мисълта ми е, че след като неговото типично изпълнение в края на всяка година е 6.00, вие лесно можете да направи увереното предположение, че следващият път вашият приятел отново ще постигне резултат 6.00. Да, нещата могат и да се объркат ужасно, и да не стане така, но това, от което ние се вълнуваме (поне за момента) е каква е вероятността ние да сме прави.

Какво представлява кривата на Гаус?

Както казах само преди няколко реда, ЕП се интересува най-вече от действията на типичния човек (като нарочно използвам думата “типичен”, а не “средностатистически”, тъй като двете са различни неща, и това ще бъде обяснено малко по-късно). Затова сега отново ще се върнем на примера с приятеля отличник, но вместо да разглеждаме неговия случай, ще се спрем на резултатите на обикновения ученик. В българската образователна система оценките варират от 2 (най-ниска) до 6 (най-висока). Чисто статистически оценката, която бива изкарвана най-често, е 4. Ако трябва да представим това под формата на графика, тя би изглеждала ето по този начин:

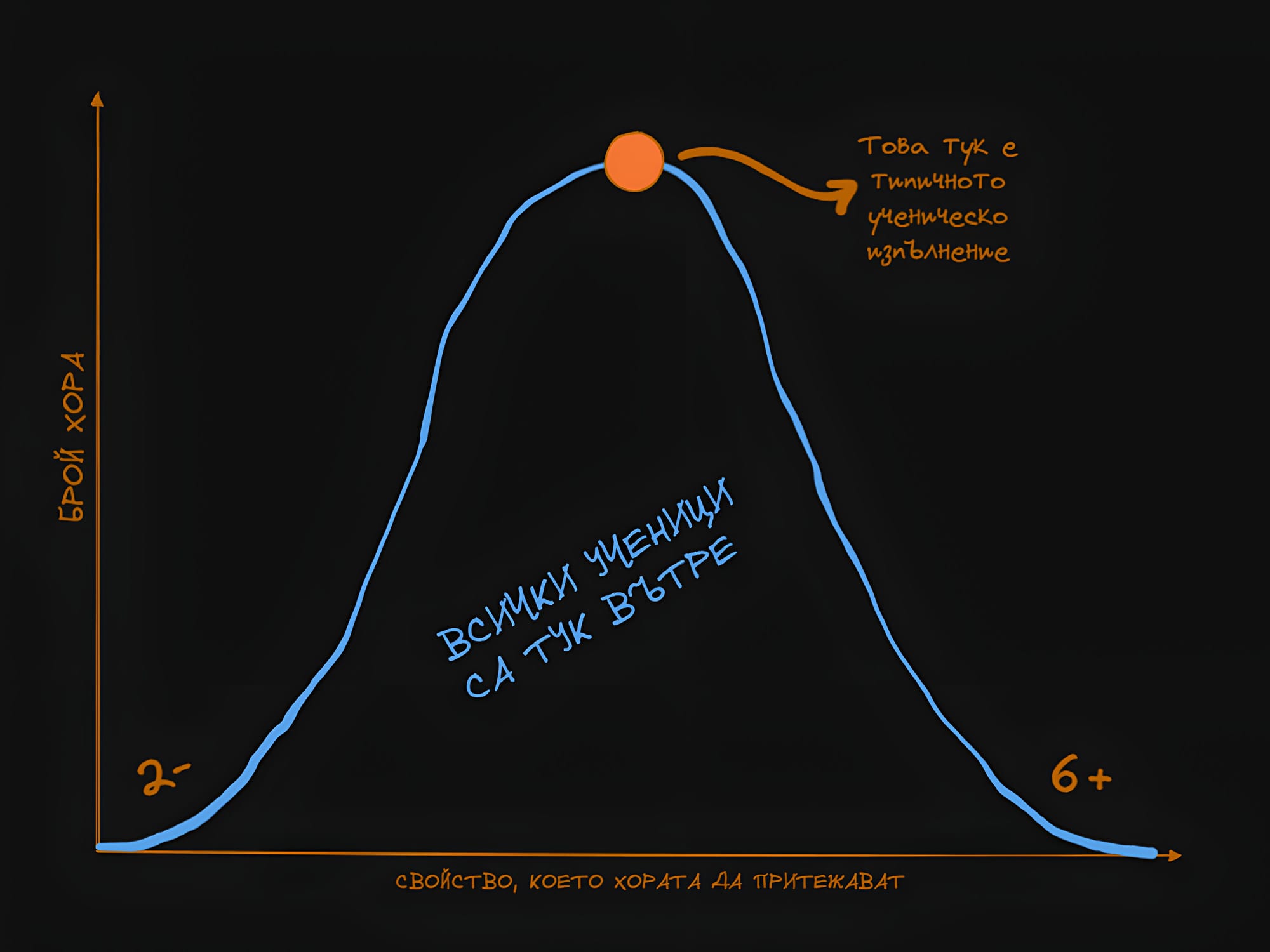
Тази графика е често срещана в различните типове науки, и е позната като “кривата на Гаус”, или още “камбановидната крива”. Под синята дъга са събрани всички членове на обществото (или поне тези от нашата извадка). Най-голям брой хора левитират около средата, и с отдалечаване от средата броят на тези хора намалява. Връщайки се на примера с учениците, това означава, че най-голям брой хора ще изкарат оценка 4, по-малък процент ще имат 3 и 5, и най-малък процент ще имат 2 и 6. Искам да обърна внимание, че тук става въпрос за това доколко реалните знания на учениците съвпадат с техните оценки (тъй като в България има склонност учителите изкуствено да завишават успеха, или пък учениците да мамят, за да изкарат по-висока оценка). Ако всичко е честно и обективно, разпределението на знания в графиката би изглеждало по подобен начин.

Къде намира приложение кривата на Гаус?

Кривата на Гаус се използва почти във всяка професионална дисциплина, в която има и числа (а в психологията има и числа, ако все още не сте го разбрали :Р). За съжаление обаче, с тази крива често се борави и доста погрешно. Ако някой икономист започне да ви говори за нея, моля ви игнорирайте го. Твърде дълго е за обяснение, но ще ви го обобщя така:
Кривата на Гаус ви показва типичното изпълнение за дадена задача. Ако дадете тази задача на 1000 души, огромна част от тях ще ви върнат средни стойности, а останалите ще бъдат разпределени в краищата. Кривата може да бъде по-тясна (например само 40% от хората връщат типичен отговор), или по-широка (90% от хората се справят по сходен начин). Желателно е кривата да бъде използвана само по въпроси, които могат ясно да дефинират спектъра от възможни отговори по тези въпроси - например когато искаме да разберем средния ръст на мъжете в България; средната стойност на IQ за жените в България; или пък доколко невротичен е типичният жител в нашето общество. Не е желателно кривата да бъде използвана в сфери, където изключенията от типичното изпълнение са много по-значими от типичното изпълнение (както е и в икономиката).

Термини от този урок:

типично изпълнение - най-обичайно срещаното изпълнение на дадена задача
Гаусова крива - процентно разпределение на възможностите за изпълнение на дадена задача